By 이태호 in Tech — Oct 10, 2025

기어의 철학

기어 설계의 철학에 대해 알아보자.

위 기어에 대해 특별히 의문을 제기할 부분이 있을까? 너무나 전형적인 기어이다. 나도 이때까지 그렇게 살아왔다. 하지만 이번에 기어를 3D프린팅하기 위해 3D모델링을 하면서 이 치형을 직접 그리게 되었고 이 부분에 궁금증이 생겼다. 이것을 제대로 이해하지 못하고서는 기어에서 나오는 수많은 개념들(pitch circle, addendum, tooth thickness, face, flank 등)을 제대로 이해하고 만들 수가 없었다.

왜 이런 네모 치형을 갖는 기어는 아이콘으로밖에 존재하지 않는걸까? 왜 다 아래 같은 오묘한 곡선 모형일까?

기어의 본질은 무엇일까? 왜 존재할까?

기어의 존재 이유

기어는 동력을 전달한다. 이 때 동력을 전달하며 힘의 크기나 방향을 바꿀 수 있다. 적당한 치형(치형(tooth shape) 기어 톱니 하나의 모양이다)을 가진 기어면 이런 것들을 모두 할 수 있다.

하지만 "고급 기어"는 동력을 일정하게 전달해야 한다.
또한, 기어는 학문이 아니라 공학이다. 이론상 동작하는 것이 아닌 실제 세계에서 동작 가능해야 한다. 즉 생산하기 쉬워야 하고 오차가 적어야 한다.

우리는 이 두 가지에 집중해보자.

Conjugate Action

동력을 일정하게 전달한다는 뜻은 무엇일까?

기어 2개가 맞물릴 때 우리가 토크를 주는 기어는 Driving Gear, 이 Driving Gear로 움직임을 당하는 기어를 Driven Gear라고 부른다.

여기에서의 가정은 Driving Gear는 일정한 각속도로 회전하고 있다. 이 때 우리가 원하는 것은 Driven Gear가 Driving Gear의 각속도와 일정한 비율로 함께 회전하는 것이다. 이 조건을 "Conjugate Action"이라고 부른다. 추가로 어떤 Driving Gear에 대해 이 조건을 만족하는 기어를 Conjugate Gear라고 한다.

그럼 Conjugate Action을 만족하는 기어 셋트를 찾아보자! 해가 하나만은 아닐 수 있다. 여기에서 생기는 추가적인 궁금증은 이런 것들이 있다. Conjugate Gear가 존재하는 Driving Gear는 어떤 조건을 갖추고 있어야 하며 이 때 Conjugate Gear는 어떻게 도출해낼 수 있는가? 이건 뒤에서 다시 다뤄보자.

Law of Gearing

Conjugate Action을 만족하는 기어 셋트를 알아내기 위해선 기어 원칙을 알아야 한다.

The law of gearing states that for gears to maintain a constant angular velocity ratio, the common normal to the contacting tooth profiles must always pass through a fixed point, known as the pitch point, on the line connecting the centers of the two gears.

풀어서 설명해보자면!

Conjugate Action을 만족하기 위해서는 치형이 닿아있는 접점에서의 법선이 반드시 두 기어의 중심을 이은 선 위에 있는 어떤 고정된 점을 반드시 지나야 한다는 것이다.

증명은 크게 어렵진 않아서 이 영상으로 첨부한다.

핵심은 기어 톱니가 컨택을 유지하기 위해서는 두 기어의 컨택한 점의 법선 속도가 일치해야 한다는 것이다. 이렇게 계산해보면, driving gear가 일정한 각속도로 회전할 때 driven gear가 일정한 각속도를 유지하기 위해선 두 기어의 중심을 이은 선 위에 있는 특정한 점 P를 모든 컨택 지점의 법선에서 다 지나가게 된다.

Law of Gearing을 만족하는 Tooth Profiles

이 원칙을 만족하는 tooth profile은 어떤 것들이 있을까?

조금만 생각해보면 무한하다는 사실을 알 수 있다. 기어의 중심 O1, O2 찍고, 우리가 원하는 기어비 r1, r2 정하고 이에 맞춰서 r2:r1으로 O1O2를 내분해서 고정점 P를 찍는다.

그리고 역으로 path of contact(접점의 경로)을 그린다. 손으로 어떻게 그려도 일반적인 범위 안에만 들어오면 이 모든 contact point에서의 법선이 P를 지나도록 기어 치형을 그릴 수 있다.

대표적인 tooth profile은 involute, cycloid, elliptical 등이 존재하고 이 이외에도 얼마든지 custom-designed tooth profile도 만들 수 있다.

위처럼 path of contact을 먼저 안 그리고 driving gear 치형을 먼저 그리고 역으로 law of gearing을 만족하도록 driven gear의 치형을 그릴 수도 있다.

생산하기 쉬운 기어

이제 우리는 "고급 기어"의 첫번째 조건을 만족했다. 두번째 조건인 생산하기 쉬운 기어를 만들어보자.

생산하기 쉬운 기어라는 뜻은 두 가지 의미를 담고 있다.

실제 물리적 제품은 우리가 시뮬레이션하는 것처럼 아주 칼 같을 수 없다. 10mm 제품을 만들면 9.9mm ~ 10.1mm 정도일 것이다. 어느 정도의 오차가 반드시 발생하고 이 오차에 대한 반응성이 크면 안 된다. Fault Tolerance를 갖고 있어야 한다.

또한 생산할 때 최대한 단일 도구로 많이 생산할 수 있을 때 효율이 좋다. 호환성이 좋으면 이것 또한 같은 제품을 더 많이 만들어도 되니 생산하기 쉽다.

Involute Gear

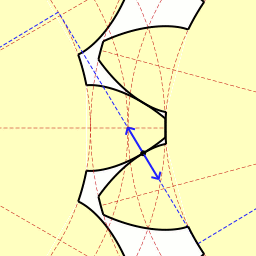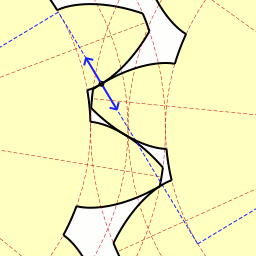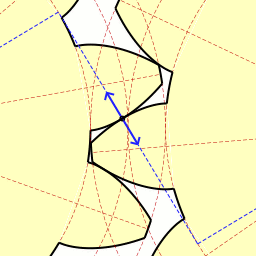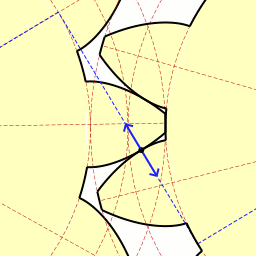
제일 유명하고 대중적이며 99% 사용하는 Involute Gear의 동작 영상이다.

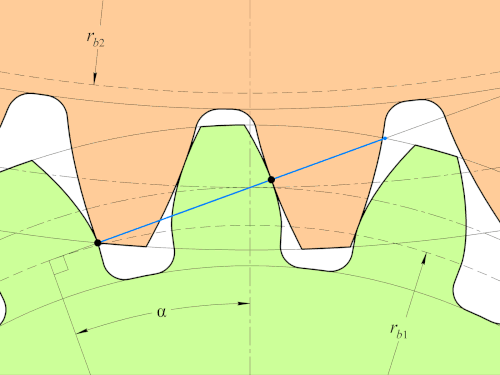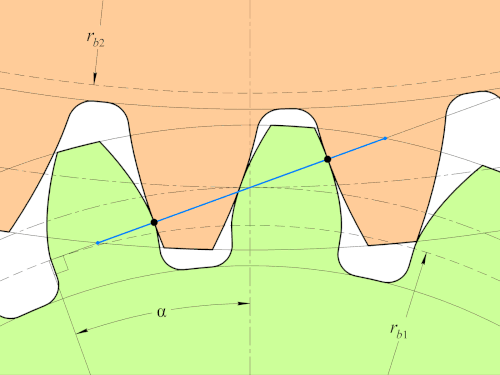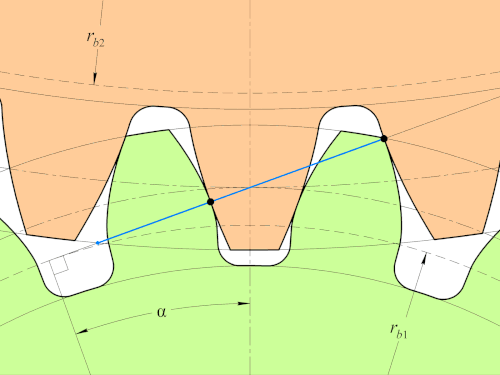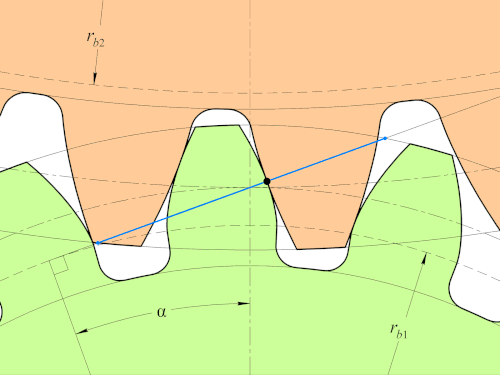
검정색 접점에서 모든 순간 법선이 정중앙에 있는 모든 점을 다 지나게 되면서 Law of Gearing을 만족하는 모습을 볼 수 있다.

또한 Path of Contact이 P를 지나는 직선임을 볼 수 있다. 이 involute profile은 path of contact이 직선이라는 특징을 갖고 있는 기어이다.

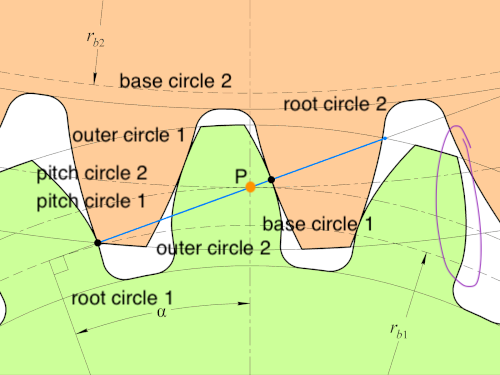
이 involute gear를 이해하기 위해 필요한 개념들이다. contact point가 base circle 1과 outer circle 2의 교점에서 시작하여 pitch circle 1, pitch circle 2의 접점이자 O1O2 위에 있는 P를 지나 outer circle 1에서 마무리한다.

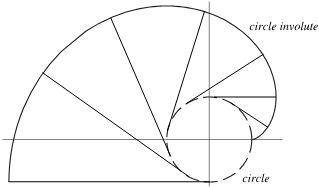
involute는 "원 위에 감겨있던 실을 풀어낼 때 그 실의 끝점이 그리는 자취"를 의미한다. 위 그림에서 우측에 있는 보라색 곡면이 involute curve이다.

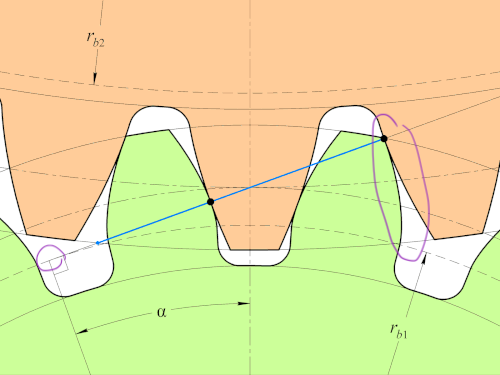
왼쪽 보라색 점부터 우측 상단 파란색 선이 끝나는 점까지 실이 팽팽하게 당겨져 있다고 하자. 여기에서 실을 쭉 팽팽하게 당기면서 천천히 base circle까지 붙이면 정확히 이 involute 곡선 형태를 갖게 된다.

이 곡선의 제일 큰 특징은 "곡선의 법선이 항상 기준원에 접한다"는 것이다. 직관적으로는 중심이 고정되어 있고 실로 돌리면 실의 끝이 원 모양을 그리는데 이 때 항상 이 원의 법선은 중심을 지난다. 비슷하게 원에 실이 말려있는 상황에서 실을 팽팽하게 펴면 법선과 실은 항상 직교하고 실은 항상 기준원에 접해있기에 이 특징이 생긴다.

확실하진 않지만, path of contact이 일직선이라면 반드시 인벌루트여야 하는 것 같다.

이 인벌루트 gif를 보고 있으면 마음이 정화가 된다.

정확하게 매 순간 일정한 압력각 알파만큼을 갖고 힘을 전달하며 접점에서 접선으로 주는 힘이 하나도 없다. 미끄러질 일이 없기 때문에 마모도 훨씬 덜하다. 기어의 치형에서 base circle부터 outer circle까지 부드럽게 접점이 바뀌며 힘을 일정하게 전달한다. 또한 매 접점에서 항상 힘을 주는 방향이 같기 때문에 접점이 조금 바뀌더라도 크게 문제 없다.

인볼루트 기어는 생산하기 쉬운 기어이기도 하다. 중심거리가 조금 떨어지더라도 압력각만 살짝 줄어들고 각속도는 여전히 일정하게 유지된다. 또한 치형을 그릴 때 압력각과 모듈만 정하면 항상 일정하기 때문에 생산하기도 쉽다.

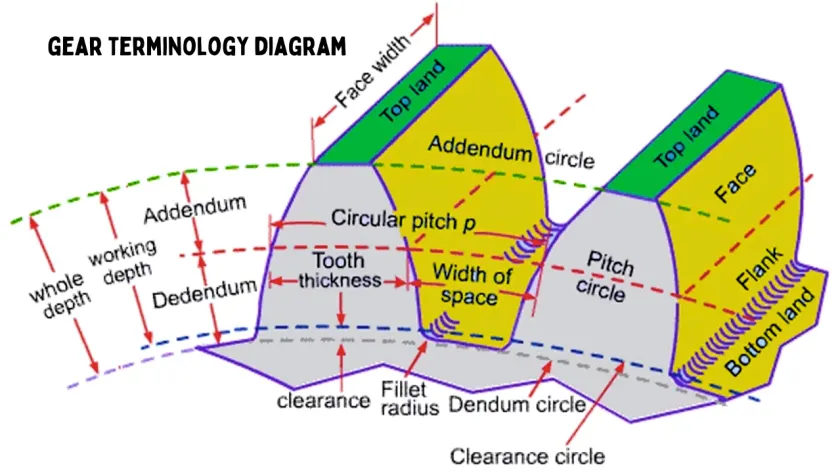
Involute Gear의 term들이다.

몇가지 중요한 텀만 정리하고 넘어가자.

teeth count Z
모듈 m
압력각 pressure angle 알파

face width, fillet radius도 정해주어야 하긴 하지만 크게 중요하진 않아 스킵했다.

먼저 teeth count를 정한다. teeth count를 정할 때는 보통 원하는 기어 비를 먼저 시스템 디자인을 통해 도출하고 이 기어 비를 만들 수 있는 정수의 teeth count Z1, Z2를 잡으면 된다.

그 다음 기어 톱니 하나의 크기를 의미하는 모듈 m을 정한다. 모듈은 pitch circle dia / Z 를 의미한다. Z는 아까 정해주었기에 자연히 pitch circle dia가 바로 나오는데 왜 여기에서 pitch circle dia를 정하지 않고 모듈을 정하는지 의아할 수 있다. 기어는 2개가 맞물리는데 이 때 맞물리기 위한 기어의 특징이 바로 이 모듈이 같은 기어여야 하기 때문이다. (당연하지만 teeth count는 같을 필요 없다.) 그래서 모듈을 먼저 정하고 각 기어에서 teeth count를 가지고 pitch circle dia를 정한다. 모듈은 기어 크기에 따라 천차만별이지만 작은 서보모터 기준으로는 1mm 정도 사용하고 (= circular pitch 3.14mm, circular pitch는 위 그림에!) 더 힘센 모터일 수록 더 큰 모듈을 사용하게 된다. 이것 또한 기어의 치근 응력식과 재료의 강도 등을 통해 좀 더 명확하게 정할 수 있다.

그 다음 압력각을 정해준다. 아까 인벌루트 기어에서의 알파이다. 14.5도, 20도, 25도 세 가지 정도의 선택지가 있지만 현재는 보통 20도로 고정이다.

인벌루트는 거의 대부분이 고정적이어서 사실 teeth count, module 2가지만 정하면 나머지는 거의 다 자동적으로 만들어낼 수 있다. 토크가 셀 때 기어가 버텨줘야 하므로 재료에 대한 고민 살짝은 필요하다. 크기가 어느 정도 된다면 웬만해서 금속류를 추천하지만 키로 정도의 크기에서는 PLA, 플라스틱으로도 충분하다.

Non-Involute Gear

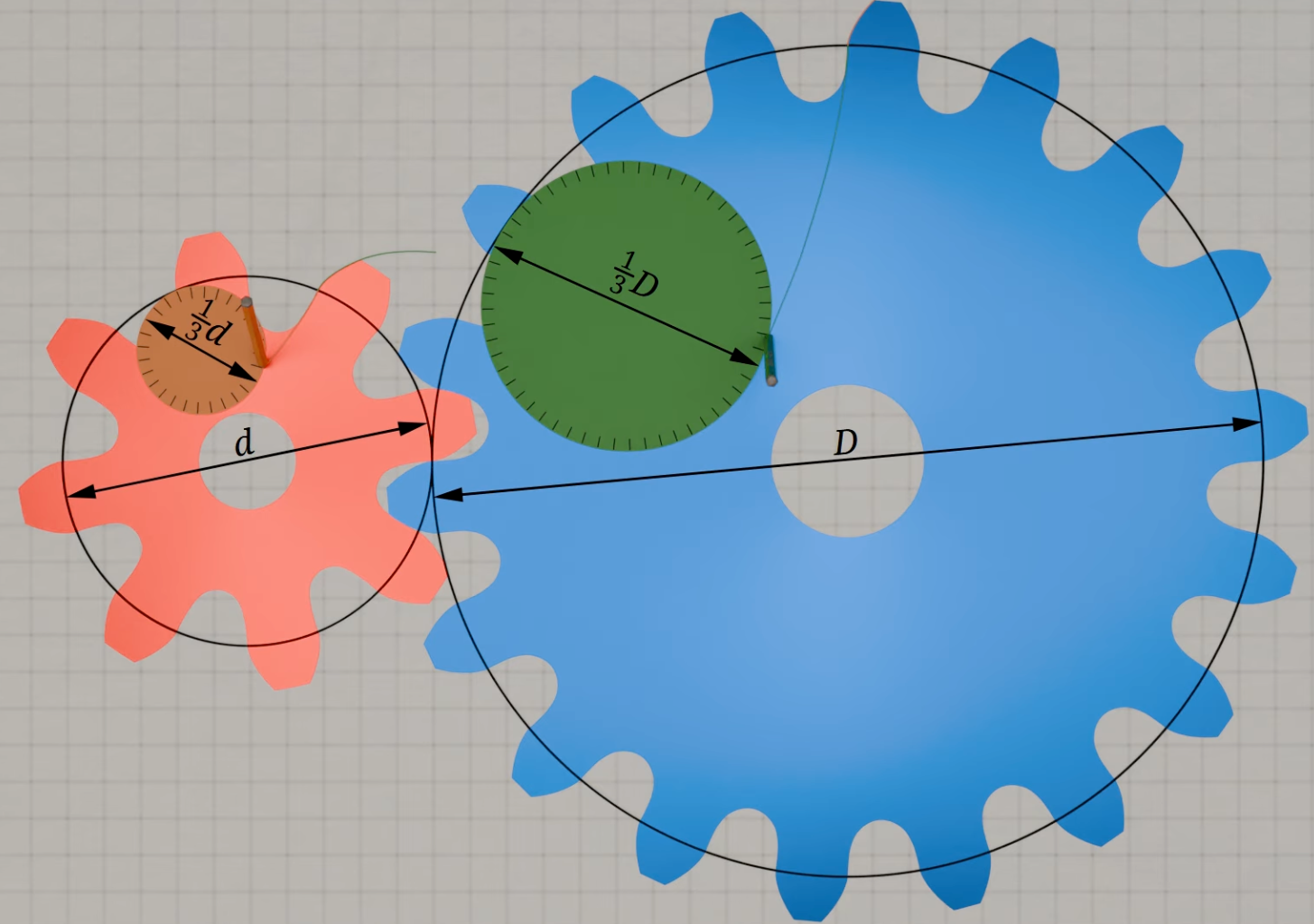
Non-involute 기어로는 이런 것들이 있다. 사실 워낙 무궁무진하다. Law of Gearing만 만족하면 되기 때문이다. 대부분 아주 제한적인 상황에서만 쓰인다.

기어의 크기나 중심거리 오차를 아예 허용하지 않거나, 생산하기 어렵거나, 호환성이 떨어지거나, 가공 난이도가 어렵거나 등등 여러 이유들로 현대에는 거의 다 인벌루트 기어만 사용한다.

결론

오늘 기어의 존재 이유, Conjugate Action, Law of Gearing, 생산하기 쉬운 기어, Involute Gear (왜 conjugate action인가?, Involute Gear의 개념들, 설계 방식), Non-Involute Gear까지 다뤄보았다.

인벌루트 기어 또한 완벽한 정답은 아니라고 말한다. 이론상 제일 완벽한 기어이지만 현실은 이와 다르기 때문이다. 하중 부하, 접촉 응력, 슬라이딩, 진동 등 여러 문제들을 현실 상에서 더 해결을 해야 한다. 더 많은 것들을 우리가 가상의 환경으로 모델링할 수 있다면 그 안에서 인류는 답을 또 찾아낼 수 있지 않을까!